Willkommen zurück auf der Entdeckungsreise, liebe DoE-Fans!

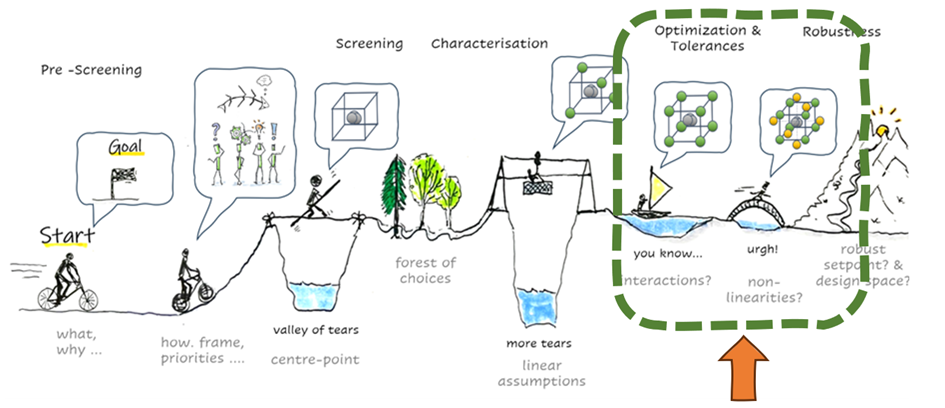
In unseren bisherigen Abenteuern haben wir uns auf die Suche nach der optimalen Einstellung innerhalb unserer festgelegten Zielvorgaben gemacht.

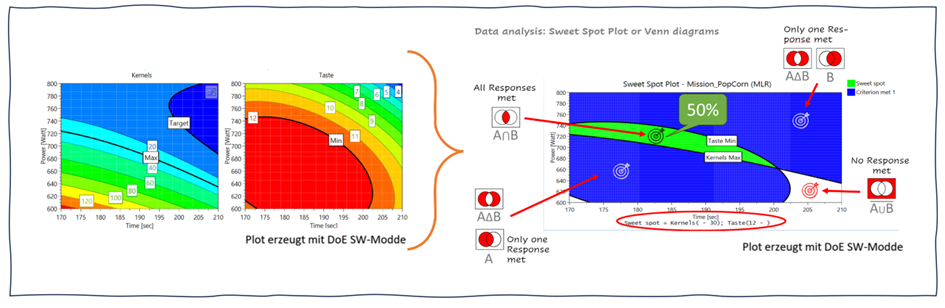
Wir haben das Terrain mit Hilfe von Venn-Diagrammen erkundet und dabei bemerkt, dass die Überlappung der Zielgebiete auf den Konturplots zwar möglich ist, ihre Aussagekraft jedoch mit Bedacht zu genießen ist.

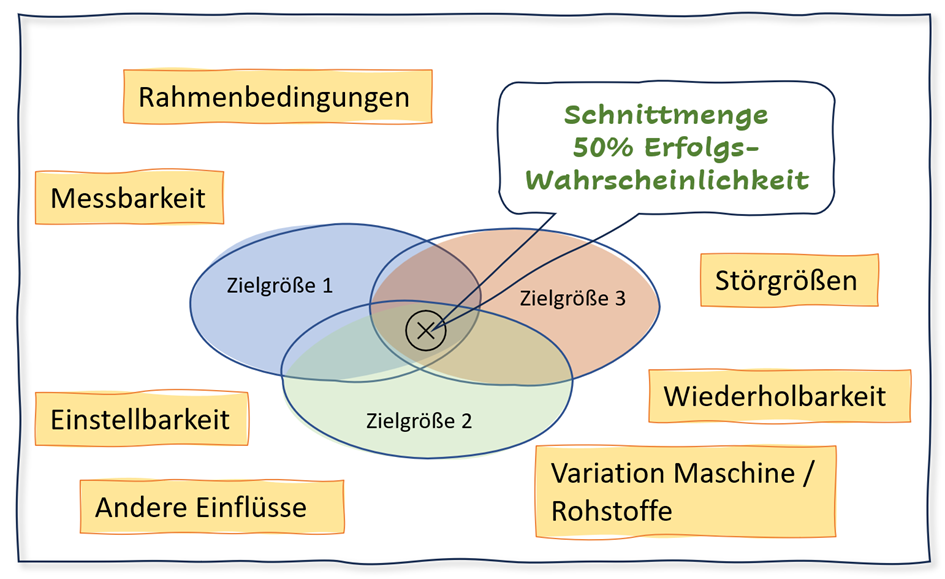
Heute nehmen wir uns die Zeit, diesen Punkt genauer zu beleuchten, insbesondere die nuancierte Bedeutung hinter der 50% Wahrscheinlichkeit, die uns bisher begleitet hat.

Es ist an der Zeit, die einzelnen Zielgrößen unter die Lupe zu nehmen:

• Jede Zielgröße wird meist durch vorher festgelegte Rahmen oder durch die Einschätzung eines erfahrenen Teams definiert.
• Die Vorhersagequalität jedes Modells variiert, insbesondere in Bezug auf die Genauigkeit und Streuung eines Zielwertes für eine gegebene Einstellung.
• Die Qualität der Vorhersagen ist nicht nur von den untersuchten Faktoren abhängig, sondern auch von externen Bedingungen wie der Reproduzierbarkeit des Versuchsaufbaus, der Messbarkeit der Ergebnisse und der Variabilität der beteiligten Komponenten.
• Zudem kann die Modellqualität durch nichtlineare, antagonistische oder synergistische Wechselwirkungen zwischen den Faktoren beeinträchtigt werden.

Mit dem „Leave one out“-Algorithmus können wir die Vorhersagegüte basierend auf durchgeführten Experimenten abschätzen, was uns hilft zu verstehen, dass nicht alle Zielgrößen gleich gut vorhergesagt werden können. Außerdem variieren die Zielgrößen in ihrer Abhängigkeit von den Faktoren, was die Komplexität weiter erhöht.

Die Herausforderung wird noch größer, wenn unterschiedliche Zielgrößen unterschiedlich gewichtet werden. Kurz gesagt, stehen wir vor einer Situation, in der drei Zielgrößen in verschiedenem Maße von den Faktoren abhängen und die Modelle sich in ihrer Komplexität unterscheiden.

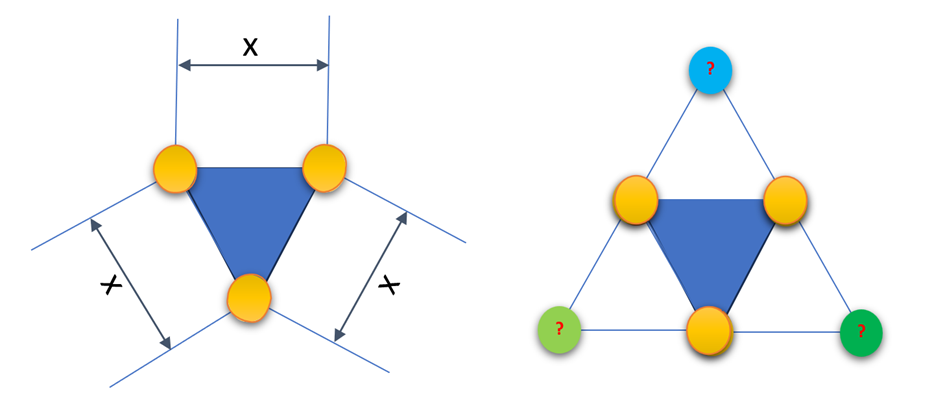
Die Lösung dieser Herausforderungen mit Standardmitteln ist oft nicht einfach. Viele Softwarepakete wie z.B. #Modde setzen hierfür auf evolutionäre Algorithmen oder spezielle Optimierungsverfahren. Als Vertreter dieser Gruppe möchte ich den Simplex-Algorithmus vorstellen, einen flexiblen und anpassungsfähigen Ansatz, der seine mathematische Form je nach Anzahl der Faktoren (Topologie des Versuchsraums) ändert.

(Übrigens wurde dieser Simplex-Algorithmus von George Dantzig in den 1940er Jahren entwickelt)

Um den Simplex-Algorithmus besser zu verstehen, betrachten wir zunächst ein zweidimensionales Beispiel, bei dem eine Zielgröße von zwei Faktoren abhängt. Hier entspricht das Simplex einem gleichschenkligen Dreieck, das an seinen Seiten gespiegelt werden kann, um dadurch neue Punkte zu bewerten. Die Länge der Seiten definiert die Schrittweite und somit die Genauigkeit der Optimierungsrichtung.

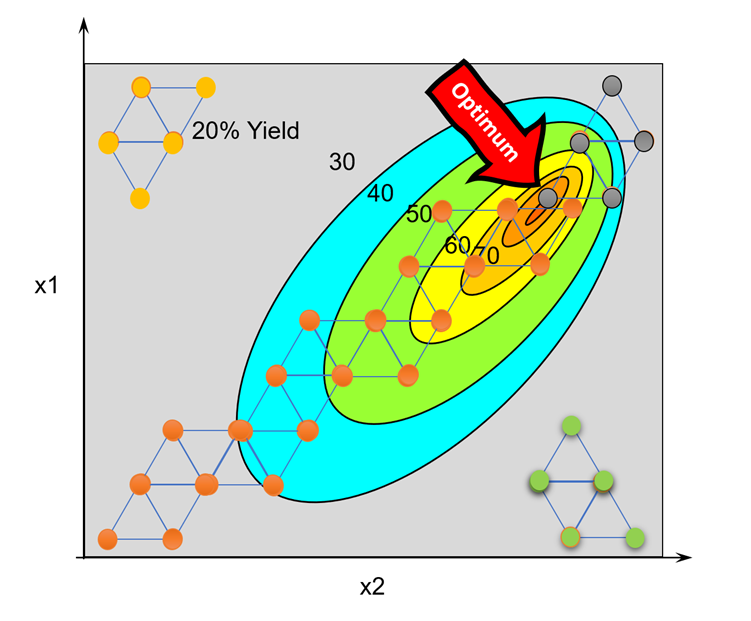
Es ist möglich, dass sich ein Simplex in einem lokalen oder globalen Maximum verirrt. Deshalb ist es sinnvoll, mehrere Simplexe gleichzeitig zu starten, um Irrwege zu vermeiden und die Suche zu optimieren. Die Priorisierung der Zielgrößen beeinflusst die Richtung des Simplex. Durch eine kumulierte Bewertung, die den Abstand zu allen Zielgrößen gewichtet berücksichtigt, kann die Optimierungsrichtung gezielt gesteuert werden.

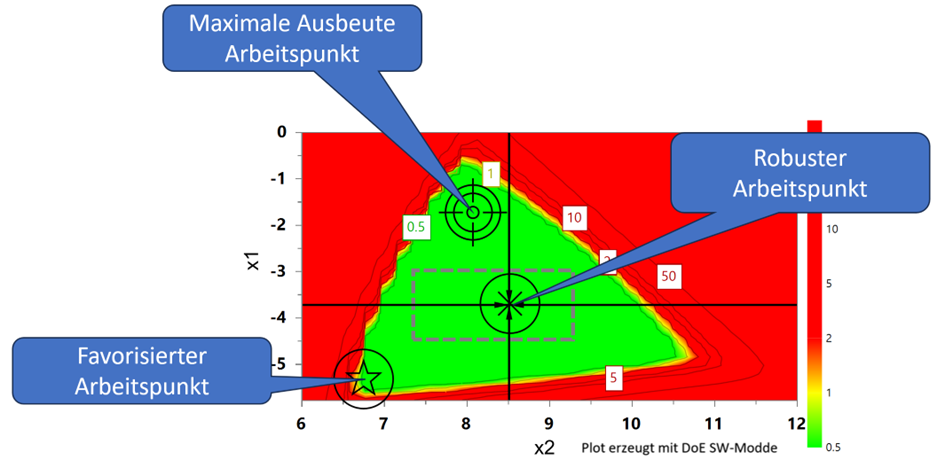
Im voranstehenden Plot sind drei mögliche Arbeitspunkte schematisch eingezeichnet, die mit den bisher besprochenen Techniken noch nicht unterschieden werden können. Daher werden wir uns im nächsten Blog mit der Monte-Carlo-Simulation auseinandersetzen und erforschen, wie wir den für uns besten Arbeitspunkt samt Toleranzen für die Faktoren ableiten können, die zu unserem „robusten“ Optimierungspunkt führen.

Bis dahin, lasst uns die Optimierung als eine fortlaufende Reise betrachten, auf der es stets Neues zu entdecken gibt. Bleibt neugierig und lasst uns gemeinsam die Grenzen des Machbaren erweitern.

Teilen Sie gerne Ihre Gedanken und Erfahrungen mit mir – gemeinsam können wir den Weg zur Optimierung meistern.

Bis zum nächsten Mal, bleiben Sie neugierig und experimentierfreudig!

Ihr DFSS und DoE Experte,

Stefan Moser