DoE-Happen #26: Der robuste Arbeitspunkt mit Toleranzen

Bild Stefan Moser DoE Journey 

Willkommen zurück, liebe DoE-Enthusiasten! In unserem letzten Abenteuer habe ich den optimalen Arbeitspunkt identifiziert, der nun als Ausgangspunkt für unsere tiefere Analyse dient. Heute führe ich Sie durch den „Design Space„, den „Normal Operation Range“ (NOR) und den „Proven Acceptable Range“ (PAR), um den robusten Arbeitspunkt unserer DoE-Modelle zu ermitteln.

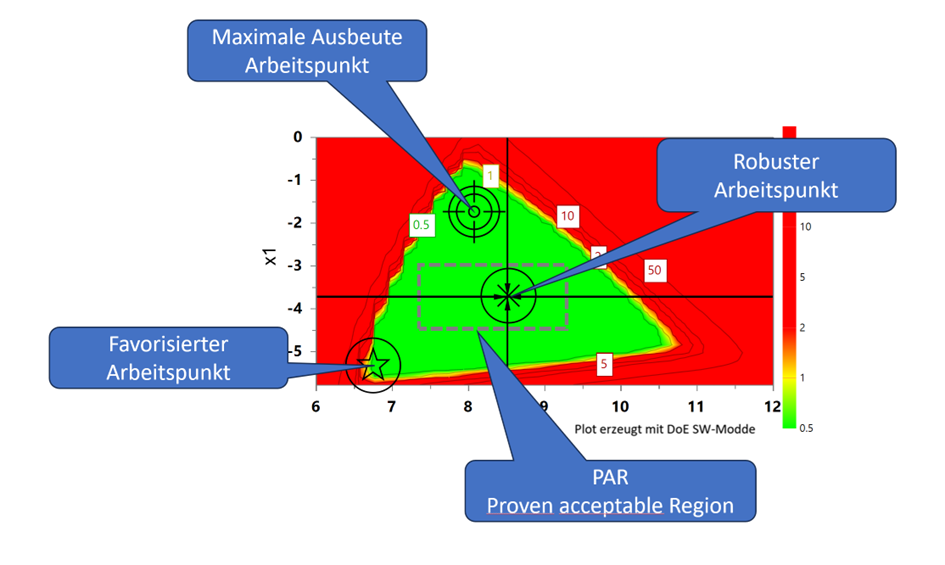
Die Ausgangsposition: Die sichere oder optimale Prozesseinstellung

Unsere Reise setzt sich fort mit den möglichen Arbeitspunkten, die wir im letzten Blog mittels des Simplex-Algorithmus erarbeitet haben. Dort haben wir für einen Prozess den normalen oder möglichen „NOR“ Normal Operation Range, also den Normalen Arbeitsbereich untersucht

Dabei haben wir folgende, grundsätzlich verschiedene Arbeitspunkte (Einstellungen für die Prozessführung) gefunden:

• 🔎Der optimale Arbeitspunkt: Bei dieser Strategie wurde während der Simplex-Optimierungen besonders darauf geachtet, alle Ziele – gemäß den festgelegten und gegebenenfalls gewichteten Prioritäten in den Spezifikationen – maximal zu erreichen.
• 🔎Der sichere Punkt: Dieser Arbeitspunkt wurde so bestimmt, dass die Wahrscheinlichkeit einer Verletzung der Spezifikationen minimiert wird. Dabei tritt allerdings die maximale Ausschöpfung der Zielgrößen in den Hintergrund.

Die Monte Carlo-Analyse – Der Weg zum besseren Arbeitspunkt!

Mit der Monte Carlo-Analyse, können wir nun die Umgebung um diesen Punkt auf Stabilität und Ausbeute/Zielerreichung untersuchen. Durch methodisches Permutieren der Faktoreinstellungen wird ein übergreifender sicherer oder optimaler Punkt ermittelt.

Der optimale Arbeitspunkt birgt immer noch das Risiko eines unsicheren Prozesssetups, weil er darauf abzielt, das Maximum aus dem Prozess herauszuholen. Wenn Sie nach dieser Einstellung suchen, um die Grenzen Ihres Prozesses auszuloten so könnte auch das ein Weg für Sie sein.

Für den sicheren Arbeitspunkt hingegen lohnt es sich, die Wahrscheinlichkeit der Nichterreichung unserer Ziele weiter zu minimieren, indem wir diesen Aspekt noch mehr Beachtung schenken.

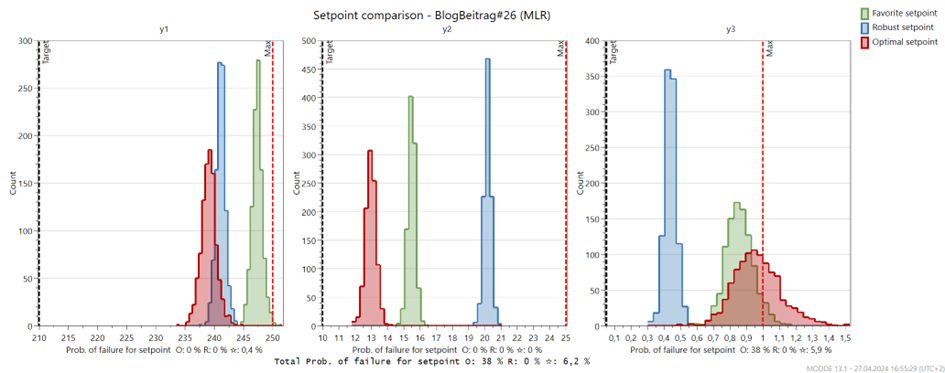
Die Arbeitspunkte im Vergleich „sicher (Robust)“, „Optimal“ und „Favorisiert“

In der Grafik sind die Arbeitspunkte für drei Zielgrößen (Links, Mitte, Rechts), die durch die Monte Carlo-Simulation ermittelt wurden, farblich markiert: der favorisierte (grün), der robuste (blau) und der optimale (rot) Set Point. Der grüne Punkt liegt nah an der Systemgrenze, was ein hohes Risiko für Grenzüberschreitungen darstellt. Der blaue Punkt weist die geringste Streuung auf und hat den größten Abstand zur Spezifikationsgrenze, was ihn zum sichersten macht. Der rote, willkürliche Punkt (Grenzwertige Prozess-Einstellung) befindet sich an der Spezifikationsgrenze, was häufige Überschreitungen der Zielgrößenspezifikationen wahrscheinlich macht. Diese Darstellung verdeutlicht die Unterschiede zwischen den Arbeitspunkten in Bezug auf Stabilität und Risiko, abhängig von den Faktoreinstellungen und deren Variabilität durch externe Einflüsse wie z.B. Einstellungsungenauigkeiten, Rohstoffschwankungen oder Maschinenabnutzung.

Vom sicheren oder optimalen zum robusten Arbeitspunkt!

Wir betrachten nun einen speziellen Unterbereich innerhalb des untersuchten Raums, in dem alle Zielgrößenspezifikationen erfüllbar sind. Der Übergang zu einem robusten Arbeitspunkt wird besonders interessant, da nicht viele Softwarepakete diese Technik unterstützen. Dieser Übergang ist bedeutsam, weil der robuste Arbeitspunkt nicht nur theoretische Zielkonformität anstrebt, sondern auch eine hohe praktische Zuverlässigkeit sicherstellt. Es ist oft herausfordernd, wenn nur Teile des untersuchten Raums die festgelegten Spezifikationen erfüllen.

Zur Veranschaulichung stellen Sie sich diesen Raum als eine Art Prozesslandschaft oder Park vor, in dem neben Bereichen mit suboptimalen Einstellungen – wo einzelne oder mehrere, aber nie alle Spezifikationen erfüllt sind – auch sichere und zuverlässige Arbeitsbereiche existieren. Die Herausforderung liegt nun darin, die Teile des Parks zu identifizieren, die nach Möglichkeit alle Anforderungen erfüllen, und gleichzeitig den Arbeitspunkt so weit wie möglich von jenen Grenzen zu verschieben, an denen der Prozess zunehmend unsicher wird.

„Manhattan Distance“-Algorithmus – Der Schlüssel zum robusten Arbeitspunkt

Als Versuchsplaner stehen wir oft vor der Herausforderung, innerhalb eines komplexen und unregelmäßig geformten Prozessraumes den optimalen Arbeitspunkt zu finden. Dieser Prozessraum kann als ein Teil eines Parks betrachtet werden, der die Fähigkeit besitzt, alle unsere Zielspezifikationen gleichzeitig zu erfüllen.

Der Vollständigkeit halber sei erwähnt das die verschiedenen Zielanforderungen auch ganz unterschiedlich von den untersuchten Faktoren abhängen können, wie z.B. die Zielfaktoren, Durchlaufzeit, Glanz, Kosten, Temperatur, Sicherheit, Festigkeit,  ….)

Die unregelmäßige Form dieses metaphorischen Parks macht es schwierig, die sichersten Bereiche auf Anhieb zu erkennen.

Um den idealen Ziel-Erfüllungsbereich innerhalb dieses Raumes systematisch zu ermitteln, teilen wir den Park in eine Matrix aus Quadraten auf. Dieses Vorgehen ermöglicht es uns, die Distanzen jedes Quadrats zu allen riskanten Grenzen dieses Zielbereiches präzise zu messen. Metaphorisch gesprochen hilft uns der „Manhattan Distance“-Algorithmus, um aus der Vogelperspektive den Punkt zu bestimmen, der am weitesten von allen kritischen Grenzen entfernt ist. Dieser Punkt repräsentiert den robusten Arbeitspunkt, der die Spezifikationen unter variierenden Bedingungen zuverlässig erfüllt. (Natürlich funktioniert dies auch für einen Raum mit mehr Dimensionen bzw. mehr als 2-Faktoren)

Zusammengefasst ermöglicht diese methodische Herangehensweise eine optimale Neupositionierung des Arbeitspunktes innerhalb der „Ziel-Erfüllungs-Fläche“. Dies gewährleistet nicht nur die theoretische Erfüllung der Ziele, sondern sorgt auch für hohe Zuverlässigkeit in der praktischen Anwendung.

Monte Carlo Simulation zur Bestimmung des robusten Arbeitsbereiches – Die Toleranzen

Die Monte Carlo-Simulation ist ein effektives Instrument, das uns ermöglicht, den Bereich um den neuen robusten Arbeitspunkt detailliert zu analysieren. Indem Faktor-Variationen simultan und unabhängig voneinander simuliert werden, können wir die robusten Grenzen oder Toleranzen der beteiligten Faktoren umfassend bestimmen. Dabei werden die Toleranzen der Faktoren zunächst so breit wie möglich und so eng wie nötig festgelegt.

💡Anpassung des „Proven Acceptable Range“ für Ihre optimale Prozessführung“

Der „Proven Acceptable Range“ (PAR) definiert den Bereich, der nachweislich sichere Bedingungen für Ihre zukünftige Prozessführung bietet. Es ist jedoch möglich, dass dieser Bereich nicht die optimale Lösung für Ihren spezifischen Prozess darstellt. Dies kann besonders zutreffen, wenn Sie in der Lage sind, bestimmte Faktoren präziser zu steuern und zu kontrollieren, als es ursprünglich durch die Simulationen angenommen wurde.

In der Versuchsplanungssoftware Modde haben Sie die Möglichkeit, diese Toleranzen individuell anzupassen. Sie können die Toleranzen enger setzen oder erweitern, je nachdem, was für Ihren Prozess am besten geeignet ist. Diese Flexibilität ermöglicht es Ihnen, die Toleranzbänder der Faktoren optimal zu gestalten und präzise zu berechnen, was Ihnen eine verbesserte Kontrolle über Ihren Prozess bietet.

Abschließende Gedanken

Es ist unerlässlich, die neu definierten Toleranzen einer gründlichen Testung zu unterziehen. Dies gibt uns nicht nur einen Einblick in das nächste Kapitel – die Robustheitsprüfung unserer neuen Toleranzen – sondern dient auch als wichtige Vorsichtsmaßnahme. Die Erfahrung lehrt, dass die vorschnelle Implementierung von Optimierungsergebnissen ohne ausreichende Verifikation oder Validierung zu unerwarteten Problemen führen kann. Daher ist es nicht nur eine Frage der besten Praxis, sondern vielmehr ein Gebot der Sorgfalt, die Robustheit der Toleranzen zu überprüfen. Schließlich kann nichts den Ruf eines Troubleshooters schneller untergraben, als wenn seine Lösungen unter realen Bedingungen versagen.

Bis zum nächsten Mal, bleiben Sie neugierig und experimentierfreudig!

Ihr DFSS und DoE Experte,

Stefan Moser

💬Falls Ihnen mein Beitrag gefallen hat, würde ich mich freuen, wenn Sie ihn teilen und ein Like hinterlassen könnten.

👉 Falls Sie Interesse an einem kompakten Online DoE Intro Kurs mit Zertifikat haben. So empfehle ich meinen folgenden Kurs.